顶点着色的魔方

---

Rubic's Cube

---

最近和同事聊起来在游戏里做魔方，有说用特效的，有说用骨骼控制器的，本着做shader的精神还是搜了下shadertoy，果然已经有先驱实践过了。大概看了下这位zackpudil的shader,主要思路就是同时计算很多个旋转矩阵，很暴力，各个矩阵和时间都是硬编码写下来的，而且shadertoy都是像素着色所以需要raymarching来显示3d结果。所以我尝试了下继承大致的思路，把计算挪到顶点着色器中，再把硬编码的部分改成利用循环自动选择轴向（开销更高但是代码简短显得有水平）。

大致描述下过程，我们在每帧都要计算6个2d的旋转矩阵，参考下图，横轴是时间，纵轴是每个矩阵的角度，左边的xyz+—是指旋转轴的朝向，也用来对旋转区域做限制。

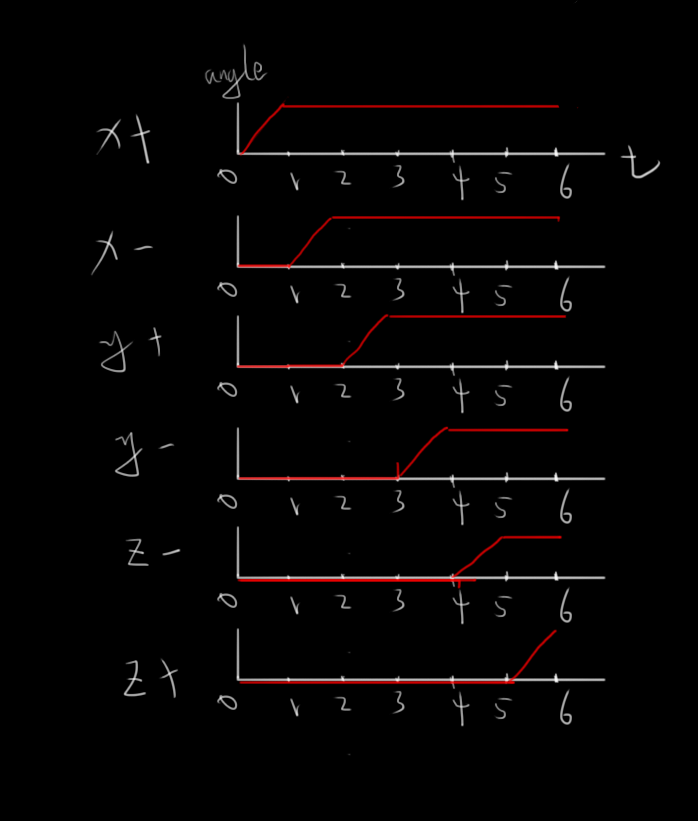
首先我们要定义一个有三个数的数组来代替本来的顶点位置,并且在每次旋转完后重新赋值。

然后同样的方式定义一个数组代表轴向，初始化值为0。
在循环中我们使用n除以2来代表轴向，用n除以2的的余数是否大于0来判断该轴的正负性。给Dir[Axis]赋值完后就得到了当前的旋转轴向，这样我们就只使用2d的旋转可以节省很大开销。
在被旋转位置坐标的选择上，分别使用n/2+1和n/2+2除以3的余数来表示会被旋转重新赋值的轴。比较难解释，可以看下图的最后两行。
至于在该轴向上对顶点的限制大家可以根据模型大小自行判断。

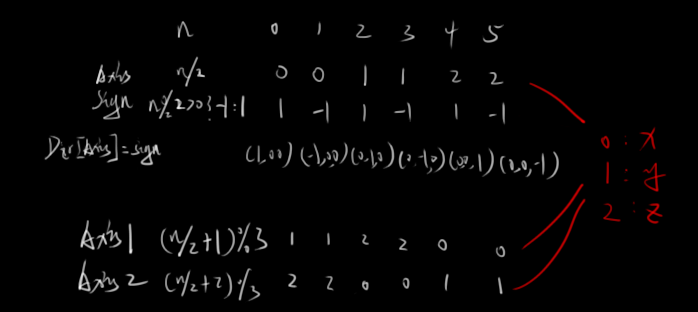
旋转矩阵的部分就不说了哈，随便百度一下‘2d旋转矩阵’都有的。下面献上完整材质连接和custom node内的内容，还是相当简洁的。声明部分放在循环外可能比较好，方便大家看（懒）我就不改了。

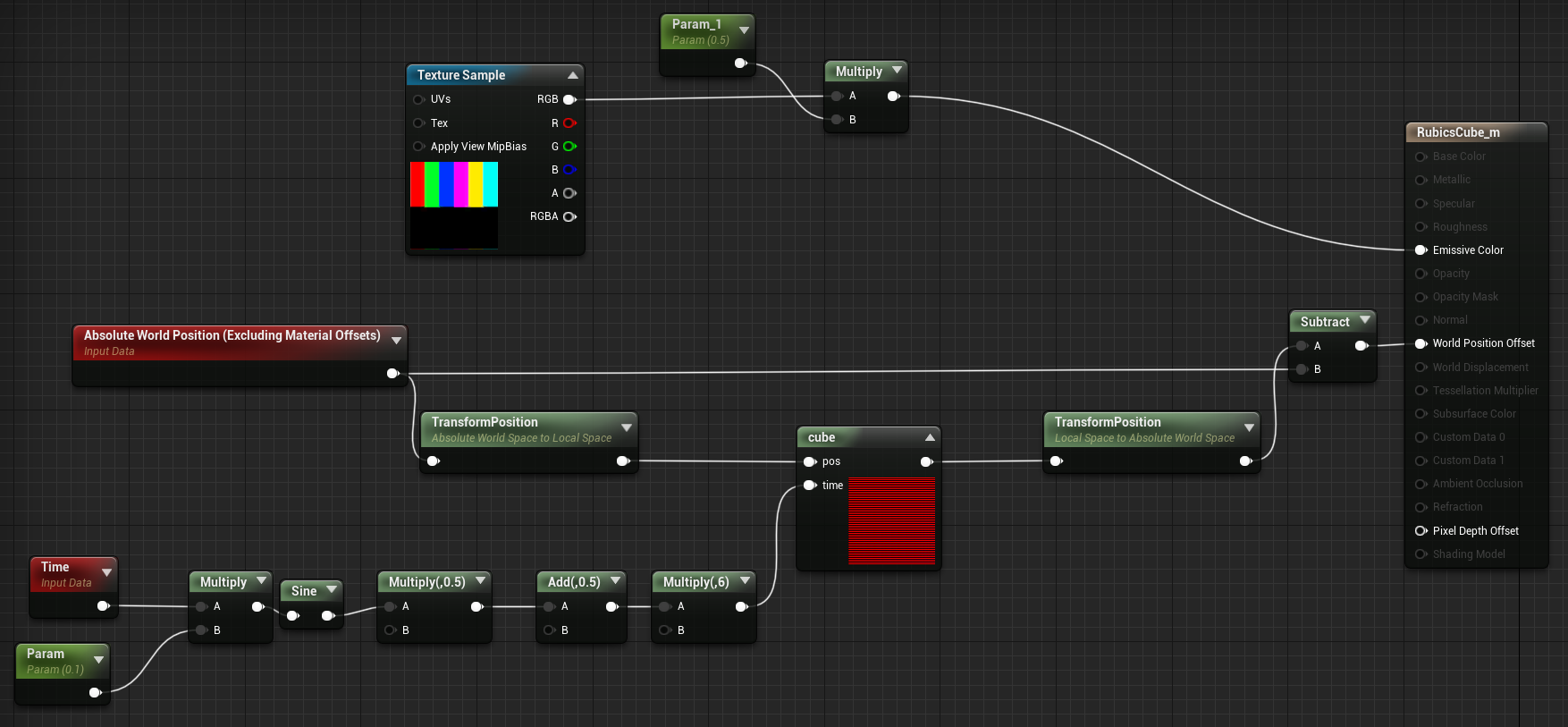
float p[3] = {pos.x,pos.y,pos.z};
for(int n = 0;n <6;n++)
{
float Dir[3] = {0.,0.,0.};
int thisAxis = n/2;
float AxisSign = n%2>0 ? -1. : 1.;
Dir[thisAxis] = AxisSign;
float3 thisDir = float3(Dir[0],Dir[1],Dir[2]);
//.66666-.5
float thisAlpha = ceil(dot(thisDir,float3(p[0],p[1],p[2]))-0.16666);
int Axis1 = (n/2+1)%3;
int Axis2 = (n/2+2)%3;

float angle = saturate(time-n)*3.141593;
angle *= AxisSign;
angle = lerp(0.,angle,thisAlpha);
//*cant write function in wpo due to redefination
float s = sin(angle);
float c = cos(angle);

float2x2 mat = {c,s,-s,c};
float2 tempP = mul(float2(p[Axis1],p[Axis2]),mat);

p[Axis1] = tempP.x;
p[Axis2] = tempP.y;
}

pos = float3(p[0],p[1],p[2]);
return pos;