二次贝兹曲线的正向距离场

---

---

用的体积雾，强行和虚幻扯点关系，改天学iq大佬做个触手把这换了

---

嗯...这次的东西有点超出了平时学习研究的范围，而且没有在搜索引擎里找到任何的相关的中文文章。事情的起因是我嘴欠在IQ大佬的shader下面问了句话，然后另一位olij大佬给我回了这么一堆的...目录。怎么办，不学不是不给大佬面子，硬着头皮上了。T.T

---

值得一提的是我再也没在shadertoy留过言了

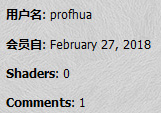
回到正题，二次贝兹曲线由三个点P0,P1,P2确定，假设P0，P2是曲线的起点和终点，对于曲线上处于t（从0到1）位置的点来说，有P(t)=(1-t)²P₀+2t(1-t)P₁+t²P₂。公式看上去十分简单，可惜我们得考虑gpu的并行处理（parallel processsing），用迭代的办法画出一个个点的位置是不切实际的。所以接下来的基本是纯数学了。

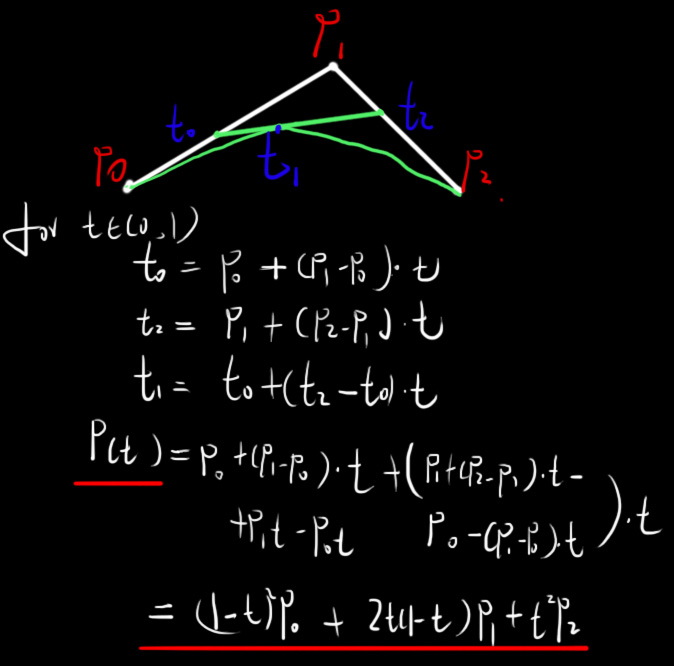
首先对P(t)求导，曲线的导数表示它的切线，P'(t)=2t(P₀-2P₁+P₂)+2(P₁-P₀)。令A=P₁-P₀，B=P₂-P₁-A。则P'(t)=2(B·t+A),然后对于屏幕上任意位置的的点M来说，M到曲线上最近点的线段是该点的垂线。垂直向量的乘积等于0，所以P'(t)·[M-P(t)]=0 → B²t³+3ABt²+(2A²+M'B)t+AM'=0,M'是P₀-M，我们令a=B²,b=3AB,c=2A²+M'B,d=AM'。则at³+bt²+ct+d=0。

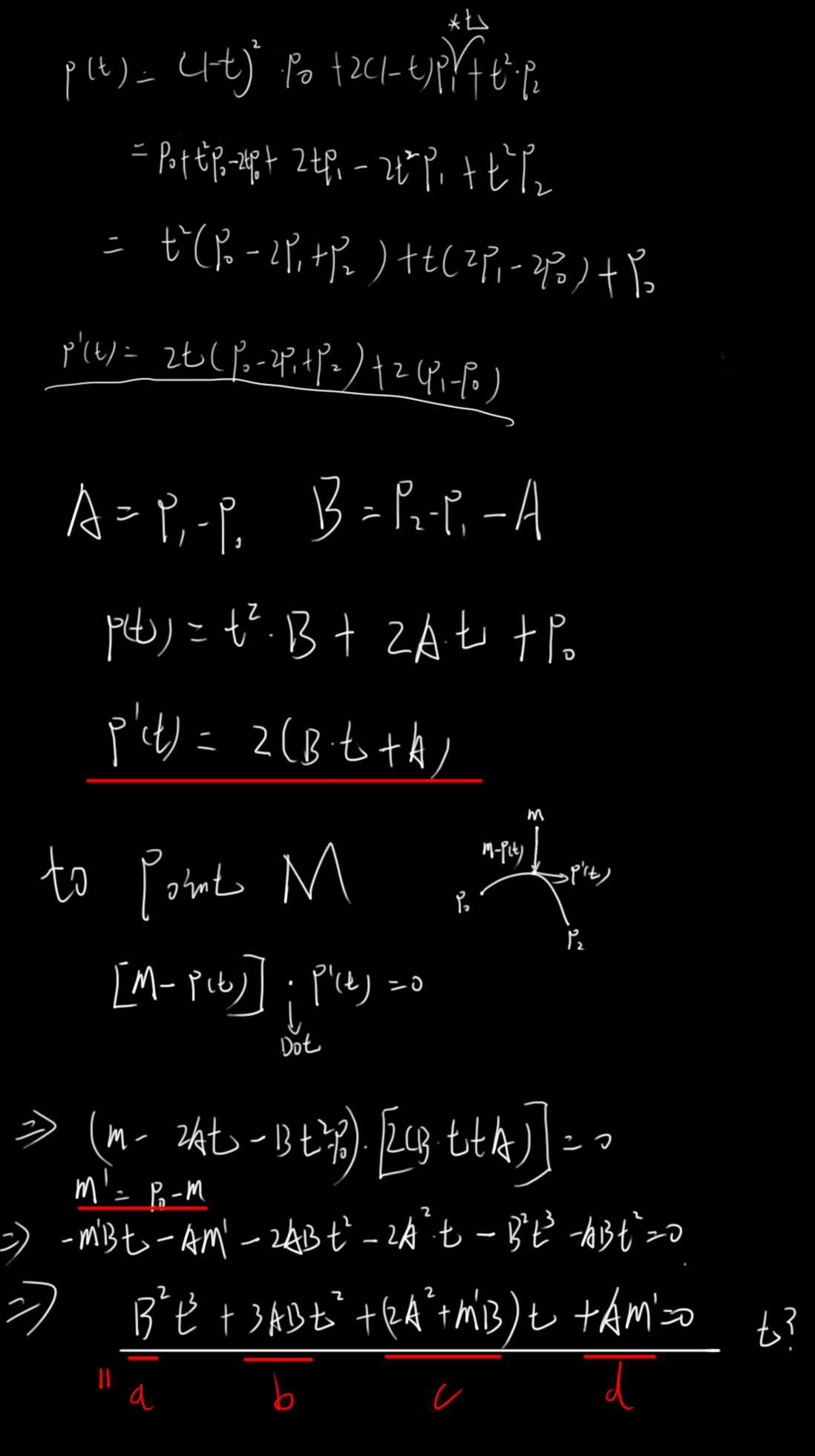
现在有了一个3次方程，求到方程的解就可以得到屏幕上各个点到曲线的最短距离。根据维基百科上的这篇文章,首先我们需要对等式进行消元得到depressed cubic，将t=t-b/3a（为书写方便，以编程的方式思考=为赋值）带入，得到t³+pt+q = 0如下图。

接下来需要用到叫做Cardano's method的方法，用u+v替代t，得到u³+v³+(3uv+p)(u+v)+q=0,我们假设3uv+p=0,会得到下图圈中的两个等式，解等式会得到u³和v³是等式z²+qz-p³/27=0的两个解。解方程得到z（也就是u³和v³）=-q/2±sqrt(q²/4+p³/27)。

查看上面解根号下的内容，当q²/4+p³/27小于0的时候，前面的方法显然不适用，没办法取巧只能解方程的3个根然后比较哪个点的距离最近。根的计算也在刚刚那篇文章中。 其中cos(a-b)=cosacosb+sinasinb，可用于减少使用三角函数次数。

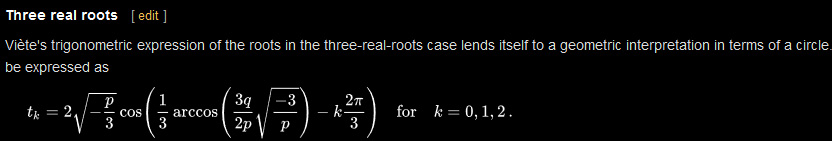
得到方程得解后向上推就可以得到离各个像素最近的曲线上的点，从而得到最近距离也就是距离场，有个距离场之后，just do whatever you want。
shader及代码如下（完全跟随步骤，需要更精简和有效率可以参考iq大佬的shader）：

---

---

precision mediump float;
varying vec4 v_Color;
uniform float itime;
uniform vec2 uRes;
//-----------|BaseUp|---------------------
float BezierSDF(vec2 M,vec2 P0,vec2 P1,vec2 P2){
vec2 A = P1-P0;
vec2 B = P2-P1-A;
vec2 Mp = P0-M;
float a = dot(B,B);
float b = 3.*dot(A,B);
float c = 2.*dot(A,A)+dot(Mp,B);
float d = dot(A,Mp);
float d3 = 1./3.;
float d27 = 1./27.;
float bda = b/a;
float cda = c/a;
float p = cda-bda*bda*d3;
float q = 2.*bda*bda*bda*d27-d3*bda*cda+d/a;
float h = q*q+4.*p*p*p*d27;
float dist = 0.;
if(h >= 0.){
h = sqrt(h);
vec2 x = (vec2(h,-h)-q)/2.;
vec2 uv = sign(x)*pow(abs(x),vec2(1./3.));
float t = uv.x+uv.y-b/(3.*a);
t = clamp(t,0.,1.);
vec2 pt = t*t*B+2.*A*t+P0;
dist = length(M-pt);
//dist *= pow((t+1.),3.608)*1.056;
}
else{
float PI = 3.1415926;
float sqrtP = sqrt(p/-3.);
float insideL = acos(3.*q/(2.*p)/sqrtP)/3.;
vec3 t = vec3(cos(insideL),cos(insideL-2.*PI/3.),cos(insideL-4.*PI/3.))*2.*sqrtP-b/(3.*a);
t = clamp(t,0.,1.);
vec2 pt = t.x*t.x*B+2.*A*t.x+P0;
float temp = length(M-pt);
dist = temp;
pt = t.y*t.y*B+2.*A*t.y+P0;
temp = length(M-pt);
dist = min(dist,temp);
pt = t.z*t.z*B+2.*A*t.z+P0;
temp = length(M-pt);
dist = min(dist,temp);
}
return dist;
}
void main() {
float t = itime;
vec4 coord = gl_FragCoord;
vec2 uv =vec2(coord.x/uRes.x, coord.y/uRes.y);
//--------------------|BaseSetting|----------------------
float sdf = BezierSDF(uv,vec2(0.2,0.5),vec2(0.50,0.50+.4*sin(itime*2.)),vec2(0.800,0.5));
vec3 col = vec3(smoothstep(.011,0.01,sdf));
gl_FragColor = vec4(col,1.0);
}

---