写一个简单SVO(稀疏体素八叉树)


SVO+Mandebort

没接触过体渲染的同学可能会对SVO有点陌生，SVO的全称是sparse voxel octree，也就是稀疏体素八叉树.


如果写过RayMarching或者MarchingCube之类算法的同学，应该都知道我们通常把空间的数据按照3D坐标存储到贴图或数组中， 但是如果空间很大的话，占用的内存就会非常恐怖了，因此SVO应运而生.


！)标题中的简单是指数据结构，该有的trace过程都还是在的.

！)没有写过cpu上的八叉树也没有关系，通常构建八叉树是为了快速查找，这里有所不同.

！)需要一些基础，比如rayBox求交这些就不详细介绍了.


·数据结构

顾名思义，稀疏指的是我们不需要把所有数据都存下来.假设空间中的离散点只有两种状态，存在和不存在.首先， 将空间切分成8份，叫做一个stack，一个stack中某一份中存在点的话，就继续切分成另一个stack， 直到切分到最小单位.将每个stack按轴向顺序当作8个连续数存到一个数组中，0表示不存在，-1表示存在且已是最小单位. 其他数字表示指向存放子stack的index，这样我们用index*8就能找到子stack的位置了.



很明显这不是一个优化结构，但是足够简单，本篇更希望专注在trace过程上.

·trace过程

首先我们明确一点，gpu上没法做递归，实际上这让trace的过程变得更加有趣了.当一条射线穿过这个3D空间的时候，我们先对最大的这个 stack进行rayBox初始化，然后找到最早进入的是8个子空间里的哪一个.



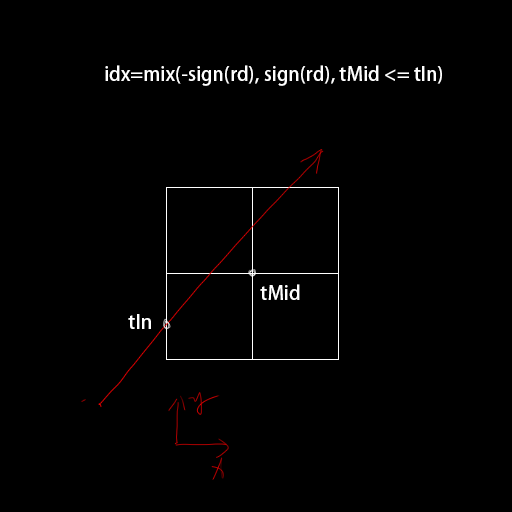
利用入射点相对中点的位置判断index

接下来就是真正核心的部分了，进入循环的过程，在射线前进的过程中我们大致需要考虑3种情况:
第一种是在一个stack内从一个子空间前进到另一个子空间，叫做advance.
第二种和第一种类似，只是在前进到另一个子空间的时候发现这个子空间也被细分过，所以我们进入这个子stack，叫做push.
第三种是从子空间向前进的时候发现已经走出这个stack的范围了，于是我们跳回母stack再向前进.

这其中判断是否走出stack范围的实现也非常巧妙,仔细尝试下各种情况可以发现当射线在stack内前进的时候idx会根据轴向向射线方向上变换, 而当出stack的时候原idx已经是射线方向,因此新idx会和旧idx相等:



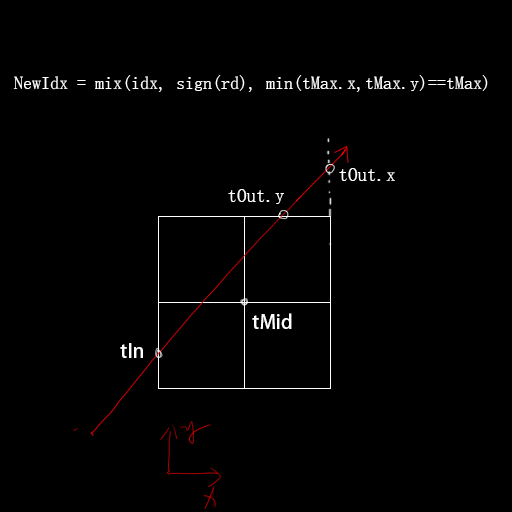
！)注意没有从一个stack直接跳到另一个邻近的stack的情况，都是pop→advance→push.


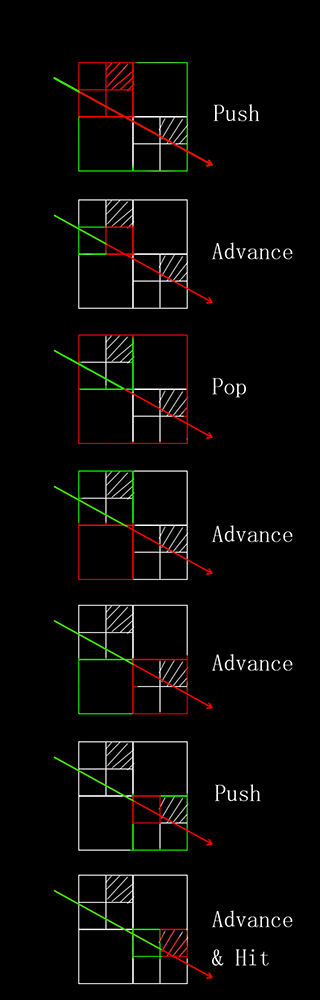
手绘了一份射线的trace过程

再放一下循环的pseudo code:

  • Initialize Base Stack
  • can_push = true
  • while(iteration count)
  •    raybox Stack[scale];
  •    if(voxel exist)
  •        if(hit the smalleset voxel)
  •        return true
  •    if(can_push)
  •        push
  •        contitue;
  •    advance
  •    get new idx
  •    if(new idx == old idx)
  •        pop
  •        can_push = false
  •    else
  •        can_push = true

    • 想了解更细节可以看NV的论文Efficient Sparse Voxel Octrees 或者我写的一份简单shader

    ·简单总结

    写这篇的初衷是因为自己学习的过程确实比较艰难,国内几乎没有资料.硬啃NV的论文语言水平有限也很吃力.再者要解释svo也是很吃力的,不过还是希望能填补上一点空白.

    本文仅仅介绍了SVO的一种trace过程,其实SVO能做的远不止于此.比如NV论文里存储contour的数据,让体素不再是方块.油管上也有给SVO做动画的大佬.
    另外SVO的构建也是很有难度和技巧的,本人最近写了个距离场贴图转SVO贴图的工具,有很多大佬也做过模型体素化的工具,仅作trace本身的话数据本身也有很多压缩的技巧.

    为了让文章不太冗长其实省去了很多细节,有实现问题的可以知乎私信我.

    总之,体渲染是个很有趣的领域,不管是这两年比较火的raymarching、svo、还是isoface的各种算法(MarchingCube,Naive SurfaceNet,Dual Contouring...)，都非常有意思.
    刚开始学c++的时候写过一次SurfaceNet，然后断断续续也看了不少Dual Contouring的算法、QEF和数学基础，最近也打算开始实践了，希望后面有机会也和大家分享,Peace.